“The enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and ... there is no rational explanation for it.” -- Eugene P. Wigner

Wikipedia entry (my emphasis):

Eugene Paul "E. P." Wigner, ... (... November 17, 1902 – January 1, 1995), was a Hungarian American theoretical physicist and mathematician.

He received a share of the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles"; the other half of the award was shared between Maria Goeppert-Mayer and J. Hans D. Jensen. Wigner is important for having laid the foundation for the theory of symmetries in quantum mechanics[2] as well as for his research into the structure of the atomic nucleus. It was Eugene Wigner who first identified Xe-135 "poisoning" in nuclear reactors, and for this reason it is sometimes referred to as Wigner poisoning.[3] Wigner is also important for his work in pure mathematics, having authored a number of theorems.

***********

Near the end of his life, Wigner's thoughts turned more philosophical. In his memoirs, Wigner said: "The full meaning of life, the collective meaning of all human desires, is fundamentally a mystery beyond our grasp. As a young man, I chafed at this state of affairs. But by now I have made peace with it. I even feel a certain honor to be associated with such a mystery." He became interested in the Vedanta philosophy of Hinduism, particularly its ideas of the universe as an all pervading consciousness. In his collection of essays Symmetries and Reflections – Scientific Essays, he commented "It was not possible to formulate the laws (of quantum theory) in a fully consistent way without reference to consciousness."

From Wigner’s “The Un­re­ason­able Effectiveness of Math­ematics in the Natural Sciences” -- pdf here. R. W. Hamming followed up with his own essay, “The Unreasonable Effectiveness of Mathematics.” Pdf here. Wikipedia.

Gregory’s Mind and Nature is one of my keepers because of its power to engage the mind in thinking. He didn’t know about epigenetics or morphic resonance, but he knew how to think in a thorough way. I enjoy this book in the same way I enjoy Jacques Monod’s Chance and Necessity, for the encounter with a first-rate mind.

In any case, it was Bateson that first brought home to me in a clear and powerful way a feeling or intuition that Plato had something right, that there is Truth beyond empirical happenings out of which our minds pull generalizations. And this Truth has its own way of manifesting in our world. The cause and effect of that process does not go from us to it, but the other way around.

At the bottom of page 83, Bateson writes, “Another mathematical example may help the reader to assimilate the effect of using two languages.

“Ask your friends, ‘What is the sum of the first ten odd numbers?’”

Then we get this:

The effect of using two languages that Bateson is after is, in one word, insight. Here is the concluding paragraph of his introduction to this section of his book, which will say the same thing another way, and thus give us insight...

In every instance, the primary question I shall ask will concern the bonus of understanding which the combination of information affords. The reader is, however, reminded that behind the simple, superficial question there is partly concealed the deeper and perhaps mystical question, “Does the study of this particular case, in which an insight develops from the comparison of sources, throw any light on how the universe is integrated?” .... (P. 76)

The two languages to compare here are mathematical versus visual. Abstract, we might say, versus visual. Let’s do the mathematical proof first.

That would start by stating the idea about odd numbers and squares this way — that for any natural number n, it is true that

1+3+5+7 ... +(2n-1) = n2.

If you’re wondering where (2n-1) comes from, that’s a way of naming the nth odd number — as in, 2n would be even, so you subtract 1 and you get the nth odd number.

OK, the way to go is to ...

 1. Check that the expression is true for the first number, 1, which we know it is.

2. ASSUME it’s true for some number after that (call it k).

3. PROVE it’s true for the next number (k+1).

A little thought shows us that in that case, the statement has to be true for all n.

So how to prove 3 if 2 ? First write the n equation with k, to get the equation we are going to assume is true for some number:

1+3+5+7 ... +(2k-1) = k2

Now put (k+1) in for k to get the next one:

1+3+5+7 ... +(2(k+1)-1) = (k+1)2

We want to show that this new equation, the next one in line, is true.

Notice that the left side of the new equation has the last part, the (2(k+1)-1), added on to the equation before that (because we’re going from the expression for k to the next one, the expression for k+1). And that means all the stuff to the left of (2(k+1)-1) is k2, so we can substitute that in and get this simpler version of things:

k2 +(2(k+1)-1) = (k+1)2

 Now we multiply things out:

k2+(2k+2-1) = (k+1)(k+1)

And we add up the left side and multiply, then multiply the part on the right to get this:

k2+2k+1 = k2+2k+1

But this is same thing = same thing, so it has to be true. So if the rule about the sum of the first n odd numbers is true for any given k, then it’s true for the next number, k+1, the k+1th odd number.

And we know it’s true for the first odd number, 1, so it’s true for the second, 3, and the third, 5, and so on through all the possible values of n we can get to by this process of adding one to the last one for which our expression () was known to be true. The math people call this proof by induction.

 ——————————————————

There is also a visual proof for this truth:

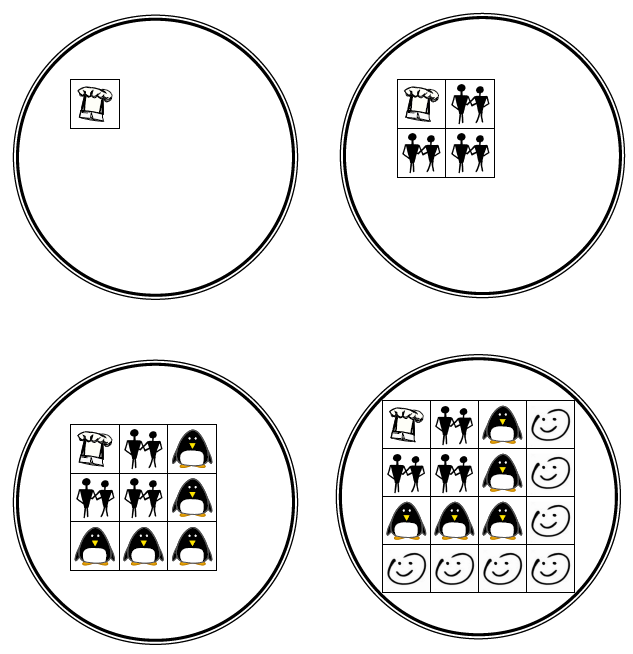
The circles group the squares of 1,2,3 and 4, corresponding to the first four odd numbers, which show in the smaller squares as 1 hat, 3 couples, 5 triangle penguins and 7 four-stroke smiley faces. The first square counts the sum of the first odd number, the second counts the sum of the first plus the second odd number and so on to the sum of the first four odd numbers. Visual inspection reveals that to make the next square in the series, the square of 5, it will be necessary to add another row and column to the square of 4 in the same manner as before, which will require 2 more small squares than we presently have smiley faces — a total of nine more small squares, nine being the next odd number. As the squares progress in size, they always add the next odd number of smaller squares to do so. We are looking at the truth that the sum of the first n odd numbers is always the square of n.

Gregory Bateson (9 May 1904 – 4 July 1980) was an English anthropologist, social scientist, linguist, visual anthropologist, semiotician and cyberneticist whose work intersected that of many other fields. In the 1940s he helped extend systems theory/cybernetics to the social/behavioral sciences, and spent the last decade of his life developing a "meta-science" of epistemology to bring together the various early forms of systems theory developing in various fields of science.[2] Some of his most noted writings are to be found in his books, Steps to an Ecology of Mind (1972) and Mind and Nature (1979). Angels Fear (published posthumously in 1987) was co-authored by his daughter Mary Catherine Bateson. (Wikipedia 20121201)

I’ve taken my math from a modern textbook partly published on the web — Book of Proof by Richard Hammack. Right here you can find the first three pages of his treatment in chapter 10 of what is called mathematical induction. He uses this odd fact about odd numbers to introduce the idea.

I made these designs for a set of coasters to give to my son and his wife one Christmas. They are both math teachers. My son tells me that he looked at them and knew right away what they meant. For any who may want to make their own coasters, I offer this pdf.